[알파고 논문 Review] Mastering the game of Go with deep neural networks and tree search

* [Nature' 2016] "Mastering the game of Go with deep neural networks and tree search" 논문을 한국어로 정리한 포스트입니다.

Mastering the game of Go with deep neural networks and tree search. (2016)

David Silver, Aja Huang, Chris J. Maddison , Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, Nal Kalchbrenner, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel, Demis Hassabis, Google Deepmind &  John Nham, Ilya Sutskever, Google.

[ 논문 ] [ DeepMind ] [ Google ]

  바둑은 거대한 search space와 바둑판 내 position ( 바둑판의 현재 상황 )과 move ( 다음 수 )를 계산하기 힘들다는 이유로 인공지능 분야에서 가장 어려운 도전 과제로 여겨지곤 했다. value network를 통해 바둑판 내 position을 평가하고 policy network를 통해 move을 선택하는 새로운 접근법을 소개하고자 한다. 이 deep neural netwrok들은 전문가 수준의 게임을 통한 supervised learning과 self-play를 통한 reinforcement learning의 새로운 조합을 통해 train된다. 또한 Monte Carlo simulation과 value network, policy network를 결합한 새로운 search 알고리즘을 소개한다. 이는 컴퓨터 프로그램이 프로 레벨의 기사를 이긴 첫 번째 사례이며, 이 전까지 적어도 백 년이 걸릴  것이라 예상되어져 왔던 업적이다.

Abstract

  바둑을 포함한 완전 정보 게임 ( games of perfect imformation )은 optimal value function $v^*(s)$를 가지며, 이는 모든 player가 완벽한 game을 한다는 가정하에  모든 바둑판의 상태 또는 state $s$에서 게임의 결과를 결정한다. 이러한 게임들은 serach tree를 통해 재귀적으로 optimal value function을 계산함으로써 해결이 가능하지만, search tree에 $b^d$ 개의 가능한 수를 포함한다. $b$는 게임의 너비 ( breadth, 가능한 move의 경우의 수 ), $d$는 게임의 평균적인 길이 ( depth )를 뜻하며, chess ($b\approx35, d\approx80$)나 특히 바둑 ($b\approx250, d\approx150$)의 경우 철저한 serach는 불가능하다. (바둑의 경우의 수인 $250^150$의 경우, 우주에 있는 원자의 수보다 많다고 한다.)

  하지만 두 가지 일반적인 원칙을 통해 search space를 줄이는 것이 가능하다. 첫 째, space의 depth는 position evaluation을 통해 줄일 수 있다. state $s$에서 search tree의 길이를 줄이고 $s$와 연결된 subtree를 결과를 예측하는 approximate value function $v(s)\approx v^*(s)$ 대체한다. 이러한 접근 방식은 인간을 뛰어넘는 performance를 다른 게임에서 보여주었지만, 바둑에서는 게임의 복잡도로 인하여 다루기 힘든 것으로 믿어져 왔다. 두 번째, search tree의 breadth는 action을 policy $p(a\mid s)$ ( position $s$에서의 가능한 move $a$에 대한 확률 분포 )를 통해 줄일 수 있다. 예를 들어 Monte Carlo rollouts은 모든 경우의 수를 계산하지 않고 policy $p$를 통해 연속된 action들을 sampling하고, 이를 평균을 냄으로써 효과적은 상황 평가를 가능하게 하였고, backgammon과 같은 게임에서 인간 이상의 performance를 보여주었다.

  Monte Carlo tree search (MCTS)는 Monte Carlo rollout을 이용해 search tree에서 각 state의 value를 계산한다. 더 많은 simiulation을 시행함으로써 search tree는 더 커지고 관련된 value는 점점 더 정확해 진다. action을 선택하기 위한 policy 또한 시간이 지남에 따라 더 높은 값을 가지는 value를 선택하게 됨으로써 향상되며, 이를 통해 policy는 최적의 play로 수렴하고, value evaluation 또한 optimal value function으로 수렴한다. 이전의 연구에서 바둑 프로그램은 MCTS를 이용하여 인간 전문가의 move를 예측하도록 train함으로써 policy를 향상하고, 이 policy를 통해 search 범위를 좁히는 데 사용하였지만, policy와 value fuction이 단순하게 Input의 선형 결합을 통해 계산된다는 한계가 있었다.

AlphaGo에 사용되는 nerual network의 구조

  최근 deep convolutional neural network ( deep CNN )는 컴퓨터 비전 분야에서 전례없는 성능 향상을 이루었다. CNN의 구조를 바둑에 적용하여, 바둑판 내 상황을 19 * 19 이미지로 전달하고, convolutional layer를 통해 바둑판 상황의 표현을 구성하였다. 를 통해 serach tree의 breadth와 depth를 줄인다. value network를 통해 현재 상황을 평가하며, policy network를 통해 action을 sampling한다. 이 neural network는 여러 단계의 machine learning으로 구성된 pipeline을 통해 train한다. 먼저 supervised learning (SL) policy netwrok $p_\sigma$를 인간 전문가의 move로 부터 학습한다. 이는 즉각적인 feedback과 high-quality gradient를 통해 빠르고 효율 학습을 가능하게한다. 또한 rollout 동안 빠르게 action을 sampling할 수 있는 fast policy $p_\pi$를 train한다. 그리고 reinforcement learing (RL) policy network $p_\rho$를 train하여 self-play의 최종 결과를 최적화하여 SL policy network 향상한다. 이는 policy로 하여금 단순히 예측의 정확도를 높이는 대신에 ( 인간 전문가의 수를 정확히 모방하는 대신 게임 자체의 승률을 높이도록 함 ) 게임을 이기기 위한 올바른 목표로 향하도록 한다. 마지막으로, RL policy network에 의해 play 되는 game의 승자를 예측하는 value network $v_\theta$를 train한다. AlphaGo는 효과적으로 MCTS와 학습된 policy network, value network를 결합한다.

neural network 학습 과정

Supervised learning of policy network

  Training pipeline의 첫 단계에서, 기존의 연구와 같이 supervised learning ( 지도학습 )을 이용하여 전문가의 수를 예측하도록 하였다. SL policy network $p_\sigma(a \mid s)$ 는 convolutional layer ( weight $\sigma$ )와 rectifier nonlinearity가 반복되는 구조로 이루어져 있으며 최종 softmax layer는 모든 가능한 수 $a$중에서의 확률 분포를 출력한다. 입력 $s$는 바둑판의 상태에 대한 simple한 표현 ( 추가 : 바둑판에 놓인 돌의 위치를 포함하여, 현재 인접한 빈 공간 등의 임의적으로 설정한 추가적인 feature들이 포함되어 있다 )이다. policy network는 랜덤하게 sampling된 state-action $(s , a)$ 쌍으로 train되며, state $s$에서 인간의 수 $a$를 선택할 확률이 최대가 되도록 stochastic gradient ascent를 사용한다.

  13-layer로 구성된 policy network를 train했으며,  KGS Go Server의 3 천만 개의 position을 사용하였다. network는 모든 test set으로부터 57.0%의 확률로 전문가의 수를 예측하였으며, 단순히 바둑판의 현재 상태와 history를 input으로 사용하였을 때 ( 임의로 설정한 feature 들을 포함하지 않았을 때 ) sms 55.7%의 정확도를 보였다. 정확도의 조그만 향상으로도 기력의 큰 향상을 보여주며, network가 클수록 더 정확한 성능을 보이지만 search과정에서 계산 속도가 느려진다. 또한 더 빠르지만 그만큼 덜 정확한 rollout policy $p_\pi(a \mid s)$ 또한 train했으며 24.2%의 정확도를 보여주지만 policy network가 action을 선택하는데 $3 ms$ ( 0.003 초 )가 걸리는데 반해 $2 \mu s$ ( 0.000002 초 )만이 소요된다.

Reinforcement learning of policy networks

  training의 두번째 단계는 policy gradient reinforcement learning (RL)을 통해 policy network를 향상시키는 것이다. RL policy network $p_\rho$ 는 SL policy networ와 같은 구조를 가지며, weight $\rho$ 또한 같은 값으로 초기화된다, $\rho = \sigma$. 현재의 policy network $p_\rho$와 랜덤하게 선택된 policy의 이전 버전이 게임을 진행한다. 상대방의 pool을 랜덤하게 함으로써 현재 policy에 overfitting되는 것을 막을 수 있으며, training이 안정화된다. reward function $r(s)$는 모든 non-terminal step $t<T$에 대해 0으로 설정되며, outcome $z_t = \pm r(s_T)$는 게임이 끝날 때의 게임이 이겼을 경우 +1, 졌을 경우 -1이 된다. network의 weights는 각 step $t$에서 stochatic gradient ascent에 의해 expectied outcome을 최대로 하도록 update 된다.

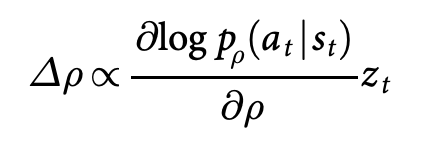
  RL polocy network는 SL policy와 게임 시 80%의 승률을 보이며,  KGS에서 아마추어 2단으로 기록된 가장 강한 바둑 프로그램 Pachi를 상대로 search 없이 85%의 승률을 보였다. 하지만 오직 CNN의 supervised learning에 의해 학습한 경우 Pachi를 상대로 11%의 승률을 보였다.

Reinforcement learning of value networks

  training의 마지막 단계는 position, 현재 상태 평가에 집중하며, value function $v^p(s)$를 계산하여 현재 상황 $s$에서 양 쪽 player가 policy $p$로 게임을 진행할 시의 게임 결과를 예측한다.

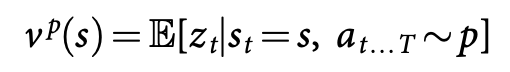
  이상적으로 우리가 알고자 하는 것은 완벽한 play에서의 optimal value function $v^*(s)$지만 실용적으로, 대신 가장 강한 policy에서의 value fucntion $v^{p_\rho}$를 추정한다. value function의 근삿값을 value network $v_\theta(s)$를 이용해 구한다, $v_\theta(s)\approx v^{p_\rho}(s) \approx v^*(s)$. neural network는 policy network와 비슷한 구조지만 output은 확률분포가 아닌 하나의 예측 값이며, valun network의 weight는 state-outcome 쌍 $(s, z)$를 이용하여 하며 stochastic gradient decent를 사용하여 예측 값 $v_\theta(s)$와 상응하는 outcome $z$사이의 mean squared error (MSE)를 최소화하도록 한다.

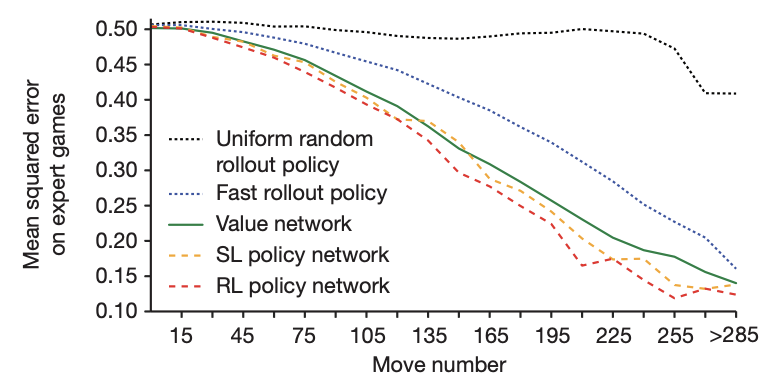
  완전한 게임을 통해 게임의 결과를 예측하는 단순한 접근 방법은 overfitting 문제를 발생시킨다, 문제는 연속된 position, 수가 강하게 연관되어 있어 단순한 돌 하나의 차이가 전체 게임에서 regression target으로 공유된다는 점이다. KGS data set을 이와 같은 방식으로 train할 경우 value network는 새로운 수에 대해 일반적인 결과를 예측하는 대신에 전체 게임의 결과를 기억해버리고 만다. 이로 인해 training set에서는 0.19의 MSE를 보이지만 test set에서는 0.37의 MSE를 달성하는 overfitting이 발생한다. 이 문제를 해결하기 위해 3천만 개로 구성된 data set을 생성하고 각각의 data를 각자 다른 게임에서 가져왔다. ( correlation 문제를 해결하기 위해 3천만 개의 상황을 3천만 개의 게임으로부터 각자 가져왔다는 뜻 ) 각 게임은 RL policy network에 의해 게임이 끝날 때까지 진행되며 이 data set에서는 각자 training set과 test set에서 0.226과 0234의 MSE를 보여주었다. 이는 overfitting을 최소화하였음을 의미한다. 다음 그래프는 value network의 상황 평가의 정확도를 보여준다. Monte Carlo rollout은 빠른 rollout policy $p_\pi$를 사용하였고 value function이 지속적으로 더 정확함을 보여준다. 또한 $v_\theta (s)$는 RL policy, SL policy를 이용한 rollout에 근접한 정확도를 보여주었다 하지만 15000배 더 적은 computation을 사용한다.

Searching with policy and value networks

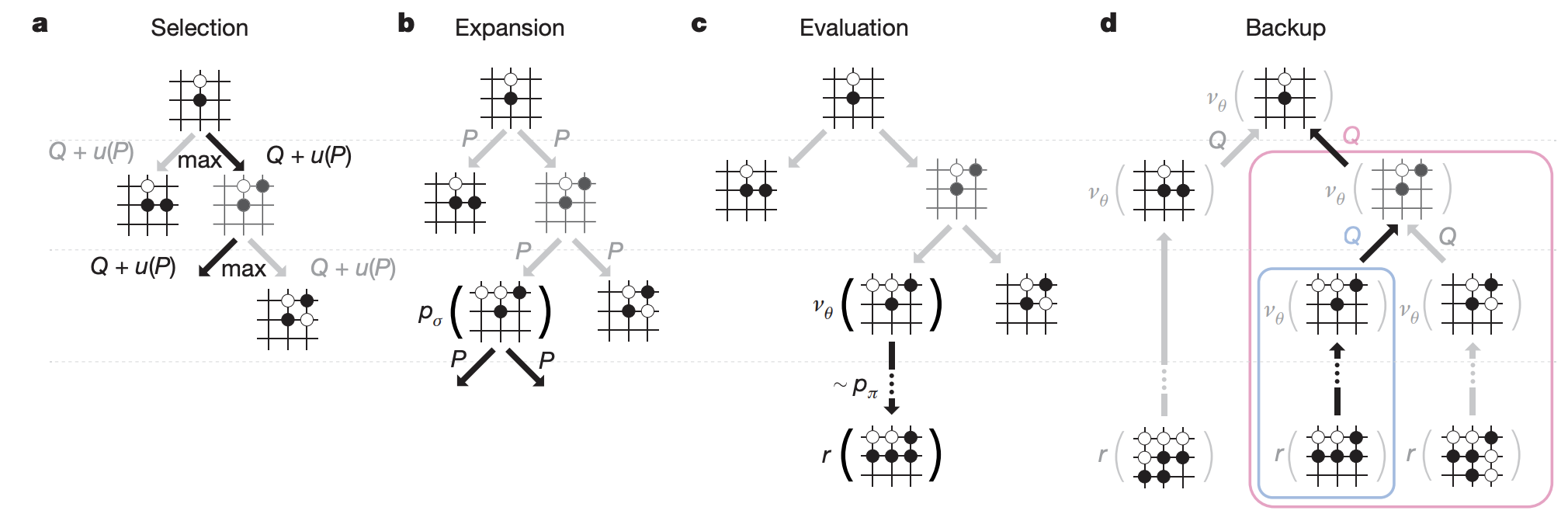
  AlphaGO는 policy netwokr와 value network를 MCTS 알고리즘에 결합하여 lookahead search를 이용해 action ( 다음 수 ) 를 선택한다. 위 그림에서 search tree의 각 edge $(s, a)$는 세 가지 값을 저장하고 있다. 1) action vlaue $Q(s, a)$ 2) visit count $N(s, a)$ 3) prior probability $P(s, a)$. tree는 simulation에 의해 root state ( 현재 바둑판의 상황 )에서 시작해 traverse된다(backup 없이 tree를 따라 내려간다.). 각 simulation의 각 time step $t$에서, action $a$는 state $s_t$에서 다음과 같이 선택된다.

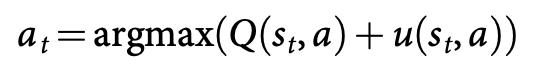
 bonus $u(s, a)$는 prior probability에 비례하지만 visit 횟수가 증가하면서 decay 되면서 exploration가 장려되게 된다. traversal이 leaf node $s_L$에 도달하면 leaf node는 확장된다. 확장은 SL policy network $p_\sigma$에 의해 한번 진행되며, 출력 확률은 prior probabilities $P$로 저장된다, $P(s, a) = p_\sigma (a \mid s)$. leaf node는 두 가지 다른 방식에 의해 평가되는데, 첫 째, value network $v_\theta (s_L)$의 output, 두 번째, fast rollout policy $p_\pi$를 이용한 random rollout에 의해 게임이 terminal step에 도달할 때까지 진행된 outcome $z_L$. 이 두 평가는 mixing parameter $\lambda$에 의해 leaf evaluation $V(s_L)$로 결합된다. (추가, rollout 또는 value network 둘 중 하나만 사용하였을 때보다, 두 방법을 반반씩 섞어 ($\lambda = 0.5$) 사용하였을 때 가장 좋은 성능을 보여주었다)

value network에 의한 값과 rollout에 의한 값을 반반 섞어서 leaf를 평가한다.

  simulation이 끝나면, action value와 visit count가 모든 방문된 edge에서 upadate된다. 각 edges는 visit count와 모든 simulation 값의 평균을 다음과 같이 축적한다.

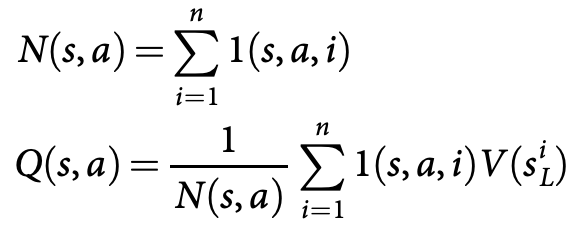
  ${s^i}_L$은 $i$번째 simulation에서의 leaf node이며, $1(s,a,i)$는 edge $(s, a)$가 i번째 simulation에서 방문되었는지를 나타낸다. search가 끝나고 나면, 알고리즘은 root position으로부터 가장 많이 방문된 수를 다음 수로 선택한다. AlphaGo가 더 강력한 RL policy 보다 SL policy를 사용할 시에 더 나은 성능을 보여준다는 사실이 주목할만 한데 ( RL policy network는 value network 생성 시에만 사용될 뿐 실제 game play시에는 사용되지 않는다! ), 이는 인간이 훨씬 더 다양한 수를 선택하는 반면, RL은 하나의 최적의 수를 선택하는데 최적화되어 있기 때문이다. 그러나 더 강한 RL policy로부터 생성된 value function $v_\theta(s)\approx v^{p_\rho}(s)$은 SL policy에 의해 생성된 value function $v_\theta(s)\approx v^{p_\sigma}(s)$보다 더 좋은 성능을 보인다.

  policy 와 value network를 평가하는 것은 전통적인 search heuristics보다 더 많은 computation을 필요로 하기 때문에 효율적으로 MCTS를 deep neural network와 결합하기 위해, AlphaGo는 asynchronous mult-thread search를 이용해 simulation을 CPU로 돌리면서 policy와 value network를 GPU에서 병렬적으로 계산한다.

Evaluation the playing strength of AlphaGo ( 알파고의 기력에 대한 평가 )

A feat that was previously believed to be at least a decade away

Discussion

  이번 연구에서는 deep neural network와 tree search를 조합한 바둑 프로그램을 개발했으며, 이 프로그램은 인공지능 분야에서 가장 큰 도전 중 하나로 여겨져 왔던, 인간 프로 레벨 수준의 플레이를 보여주었다. Supervised learning과 Reinforcment learning을 새롭게 결합하여 train한 deep neural network를 통해 최초로 바둑을 위한 효율적인 수 선택과 상황 평가 function을 개발하였으며, neural network evaluation과 Monte Carlo rollout을 성공적으로 결합한 새로운 search algorithm을 선보였다. AlphaGO는 위와 같은 요소들을 high-performance tree search engine에 통합하였다.

  Fan Hui와의 게임에서 AlphaGo는 체스에서 Ksaparov를 상대한 Deep Blue보다 수 천배 적은 position을 평가하였으며, 이는 position을 policy network를 통해 더 똑똑하게 선택하고, value network를 통해 더 정확하게 평가하였기 때문이다. 이러한 방식은 아마 더 인간의 플레이에 가까울 것이다. 더 나아가 Deep Blue가 handcraft된 evaluation function을 사용한 것에 비해, AlphaGo의 neural network는 일반 목적의 supervised learning 방식과 reinforcement learning 방식을 통해 순전히 gameplay를 통해 학습된 것이다.

  바둑은 인공지능이 직면한 많은 어려움의 대표적인 예시이다. 도전적인 의사 결정 과정, 다루기 힘든 크기의 search space, 그리고 policy와 value function을 이용해 직접적으로 접근하기에는 지나치게 복잡해 불가능해 보이는 최적의 solution. 이전의 컴퓨터 바둑 프로그램의 주된 해결책은 MCTS의 도입였고, 이는 일반적인 게임 플레이, 고전적인 planning, partially observed planning, 스케쥴링, constraint satisfaction과 같은 다른 영역에서 진전을 야기하였다. tree search와 policy, value network를 결합함으로써, AlphaGo는 바둑에서 프로수준에 도달하였고, 다른 다루기 힘든 인공지능 영역에서도 인간 수준의 performace에 도달할 수 있다는 희망을 제시하였다.